Research
Professor Costanzo’s research in computational mechanics has focused on the development of computational tools rooted in the physics of the problems. Please explore the links below for an overview of his research:
Significant Research Accomplishments
Professor Costanzo’s research in computational mechanics has focused on the development of computational tools rooted in the physics of the problems.The following publications highlight his most recent major accomplishments in research.
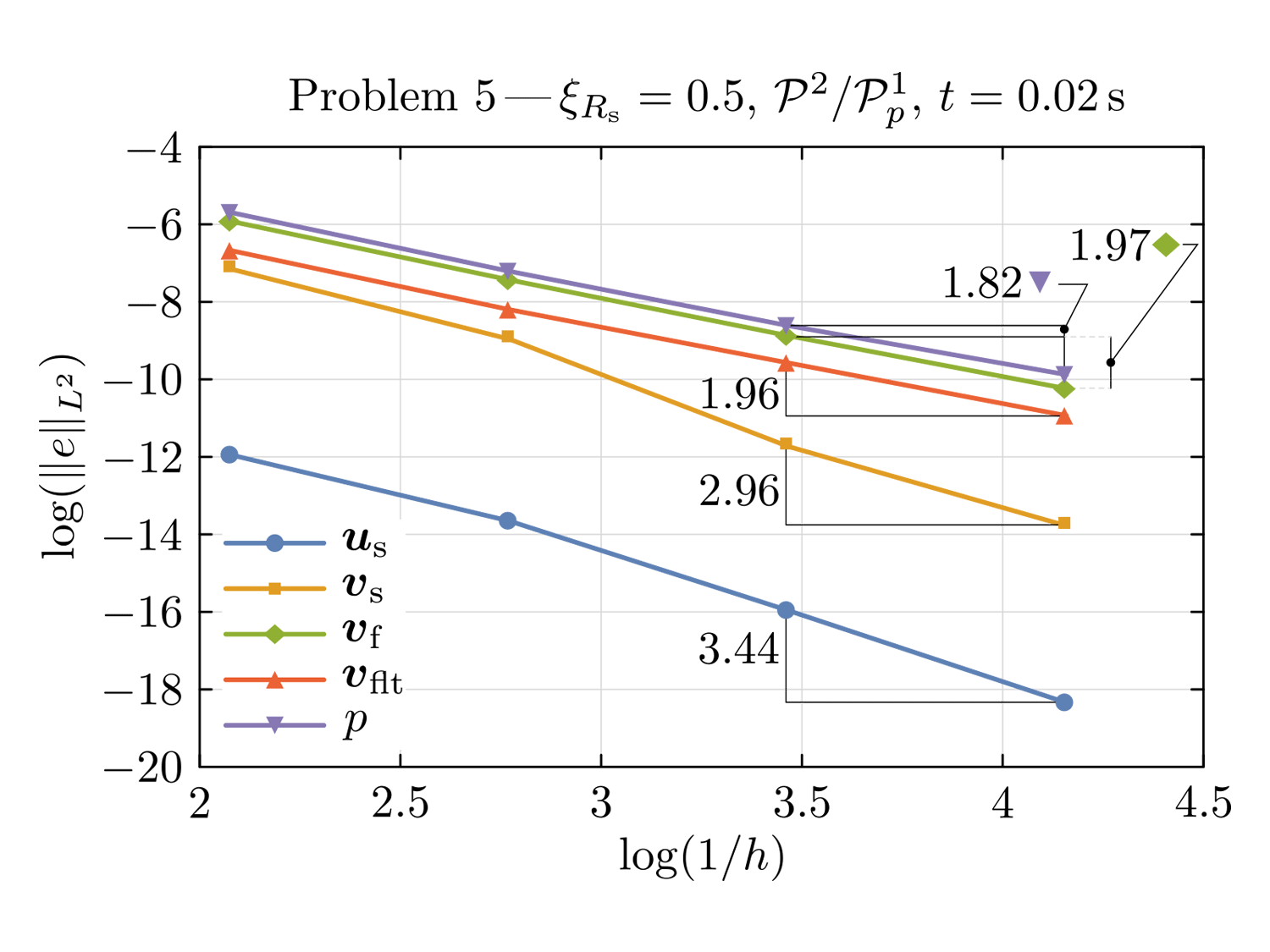
An Arbitrary Lagrangian–Eulerian Finite Element Formulation for a Poroelasticity Problem Stemming from Mixture Theory
A central problem in brain physiology is the transport of metabolites produced by cell func- tions in brain tissue from their production site to the main cerebrospinal fluid compartment. The modeling of these transport phenomena has traditionally focused on Fickian di usion within the extracellular space. More recent studies point to the existence of pathways for metabolite exchange with significant convective transport. Furthermore, evidence indicates that such convective component is driven by the pulsatile motion of arterial walls along the various elements of the brain vascular tree. These hypotheses need to be tested both against basic physiological and metabolical processes that rely on transport in brain parenchyma. They must also be tested against the mechanics of both di fusion and convection. This paper is the first rigorous result in the formulation of a stable and accurate numerical framework that can sort out the relative importance of the convective and di usive contributions to transport in brain by resolving the individual velocity fields of the interstitial fluid, vs. that of the surrounding tissue, vs. that of possible specific ionic species or neurotransmitters that one might be interested in tracking. This paper is foundational and future work will focus on testing adding di usive transport and considering physiological relevant scenarios to be com- pared with experiments. The National Science Foundation recently recommended for funding a project with F. Costanzo as the PI to complete the task in question.
Source:
Costanzo F. and S. T. Miller (2017), “An Arbitrary Lagrangian–Eulerian Finite Element Formulation for a Poroelasticity Problem Stemming from Mixture Theory”, Computer Methods in Applied Mechanics and Engineering, 323, pp. 64–97, DOI: 10.1016/j.cma.2017.05.006.
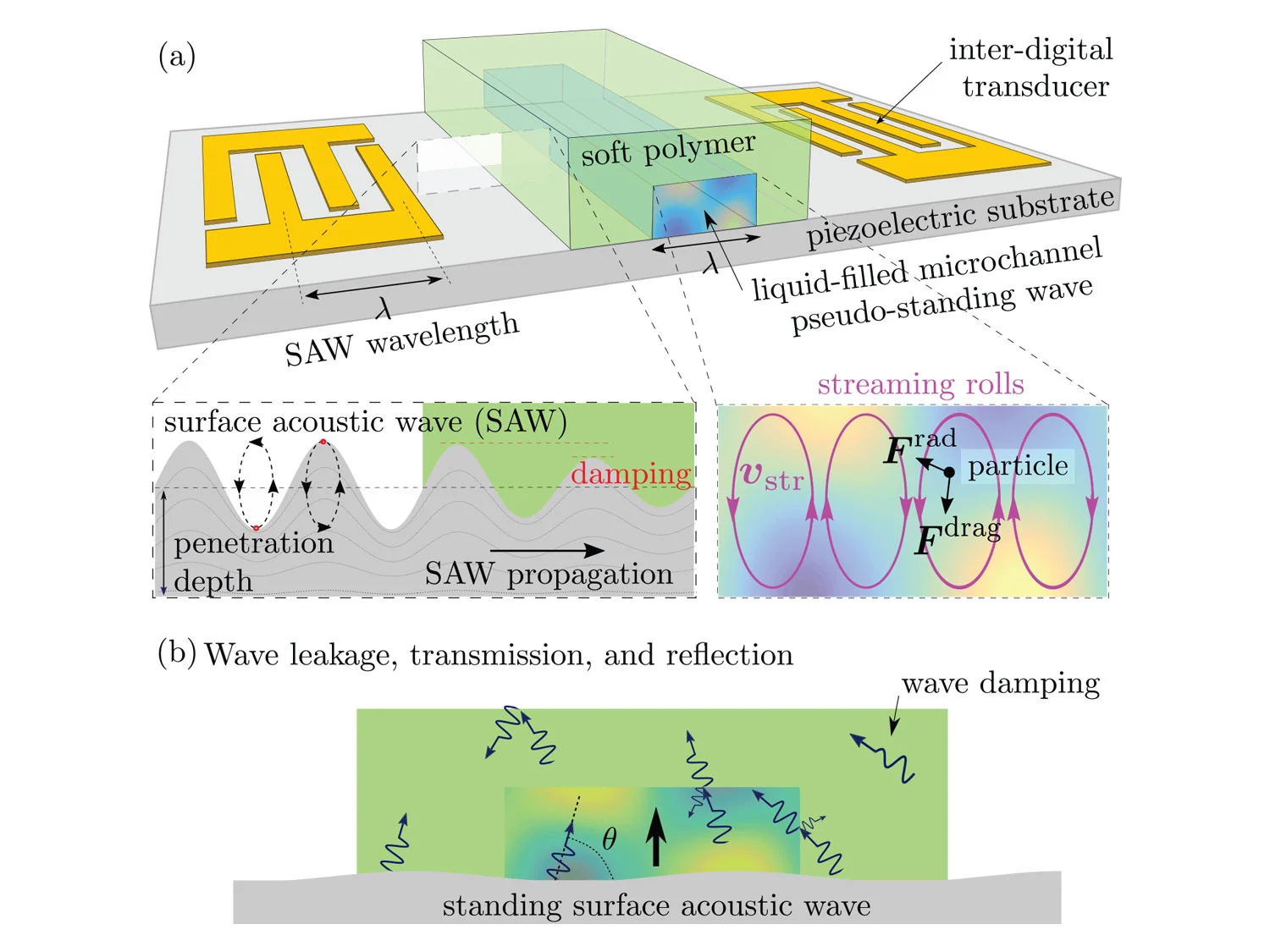
Acoustic Streaming: A Lagrangian– Eulerian Perspective
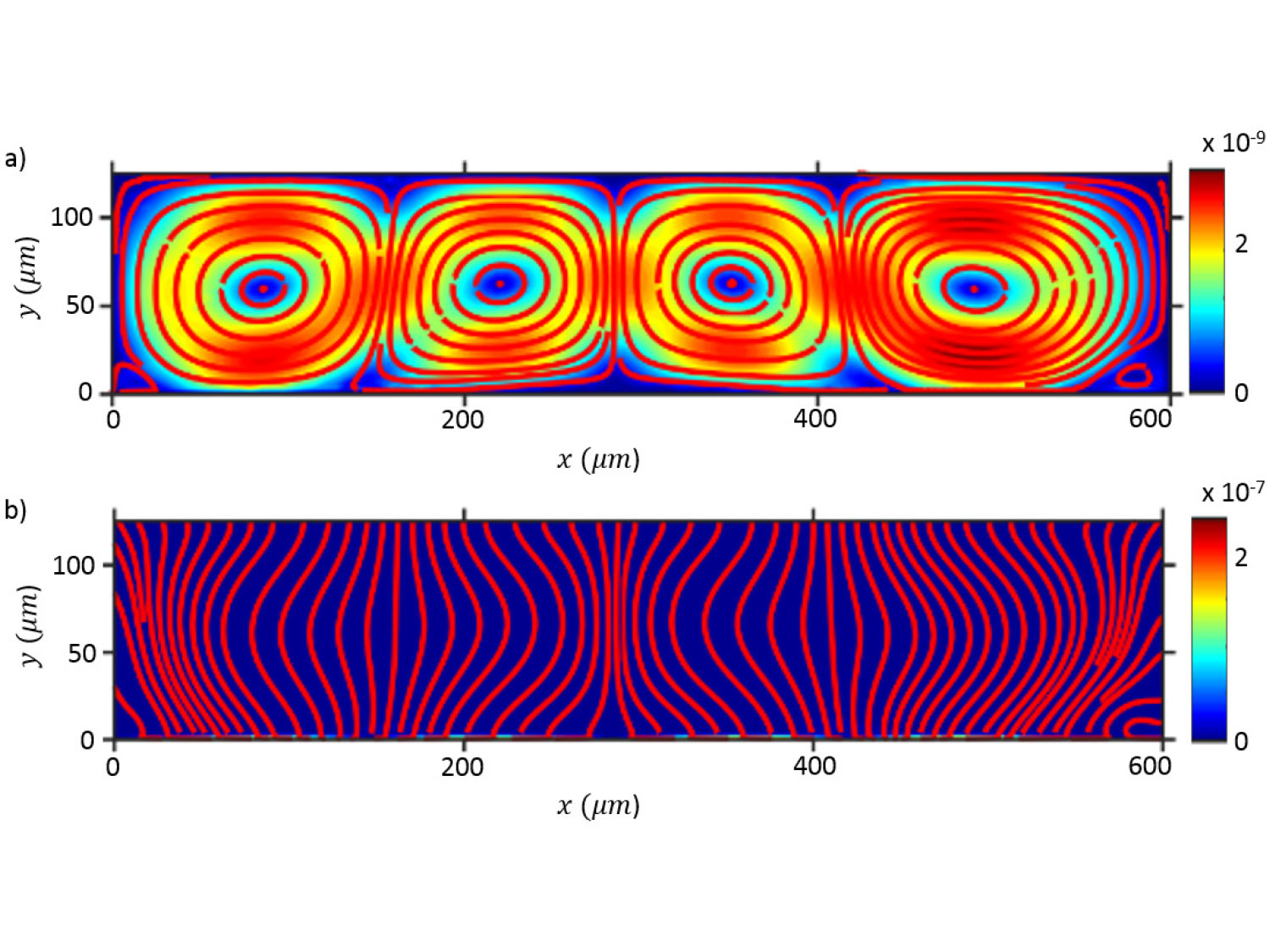
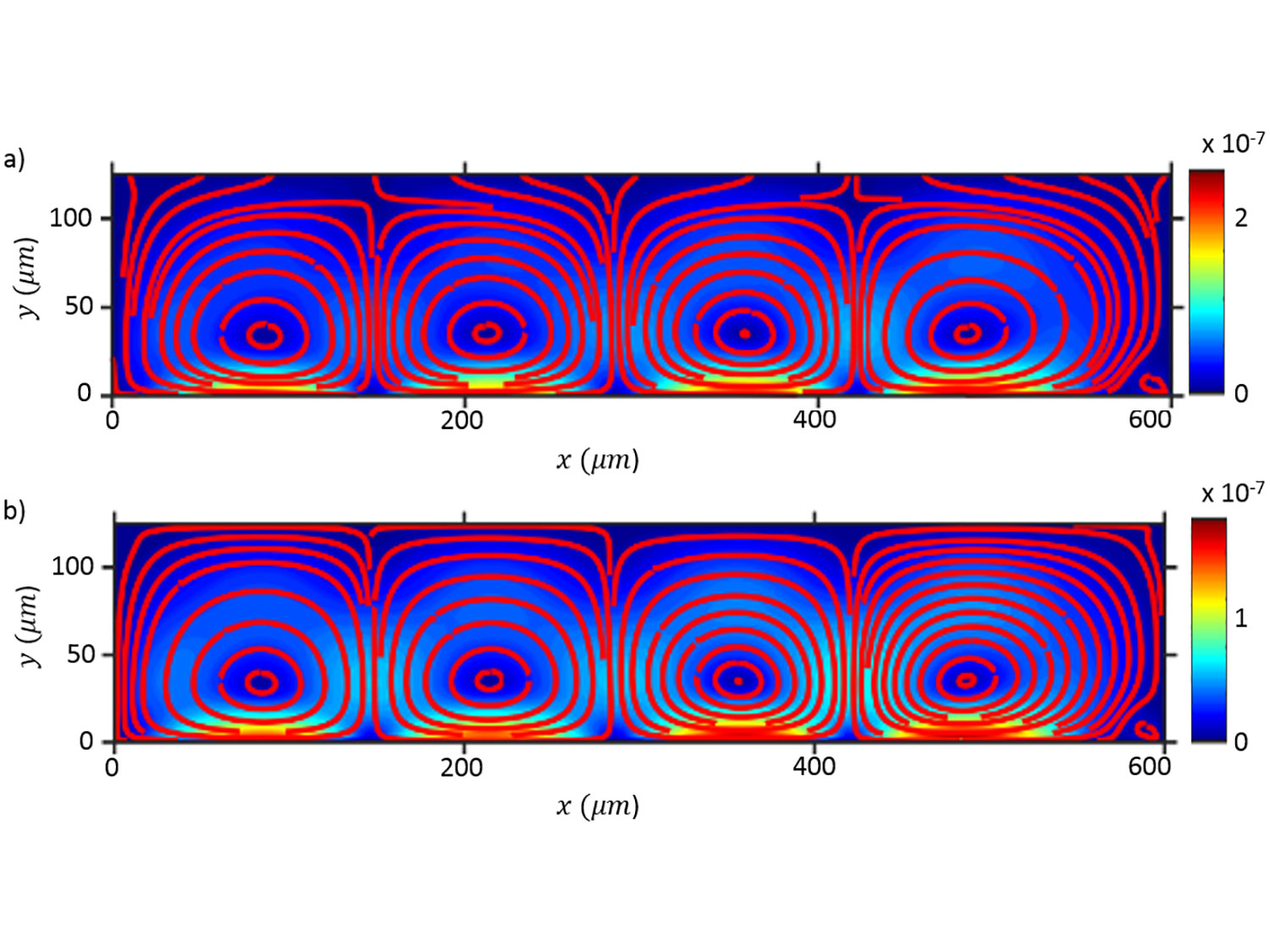
The propagation of acoustic waves in fluids is the basis for a plethora of lab-on-a-chip applica- tions, with the consequent prospect of revolutionizing point-of-care diagnostics in biomedical applications. While there have been many recent reports on the physics in confined reso- nant chamber, the physical understanding of acoustically-driven fluid and particle motion in confined leaky systems is limited. Not only is there a strong need for a mathematical and numerical framework in support of the devices in question, but there is also a need for the identification of “canonical” or benchmark experiments that can be used to validate the the- oretical framework. This paper lays the foundation for the analysis of microacoustofluidics by switching the framing of the problem from its traditional Eulerian view to an arbitrary Lagrangian-Eulerian formulation. This may seem a simple reformulation without modification of the underlying physics and therefore an exercise without much practical merit. However, this is not the case. Theoretical microacoustofluidics is, at its core, a homogenization prob- lems in time. Specifically, it consists in identifying dominant space and time scales and then using asymptotic expansions to create a cascade of boundary-value problems whose orders are defined by the separation of the identified scales. When used in practice, these expansions are truncated so as to consist of only on a finite number of problems. Therefore, the prob- lems generated by di erence kinematic frameworks yields di erent problems. In this paper we argue for the first time that an ALE perspective allows one to provide transparency to the boundary conditions used, the latter being only approximate in Eulerian formulations. In addition, the ALE formulation yields governing equations for the slow streaming that have less stringent regularity requirements compared to those yielded by the Eulerian framework. In very recent work, we have already provided practical results that demonstrated that the ALE formulation of the problems yields qualitative and quantitative results that are much closer to experimental results, so much so that the identification of an experimental bench- mark problem seems now within reach. Furthermore, we have demonstrated improved orders of convergence of the correspondent numerical implementation.† Continuation of this work in ongoing and corresponding publications are under review and in preparation.
Source:
Nama, N., T. J. Huang, and F. Costanzo (2017), “Acoustic Streaming: A Lagrangian– Eulerian Perspective”, Journal of Fluid Mechanics, 825, pp. 600–630,
DOI: 10.1017/jfm.2017.338.
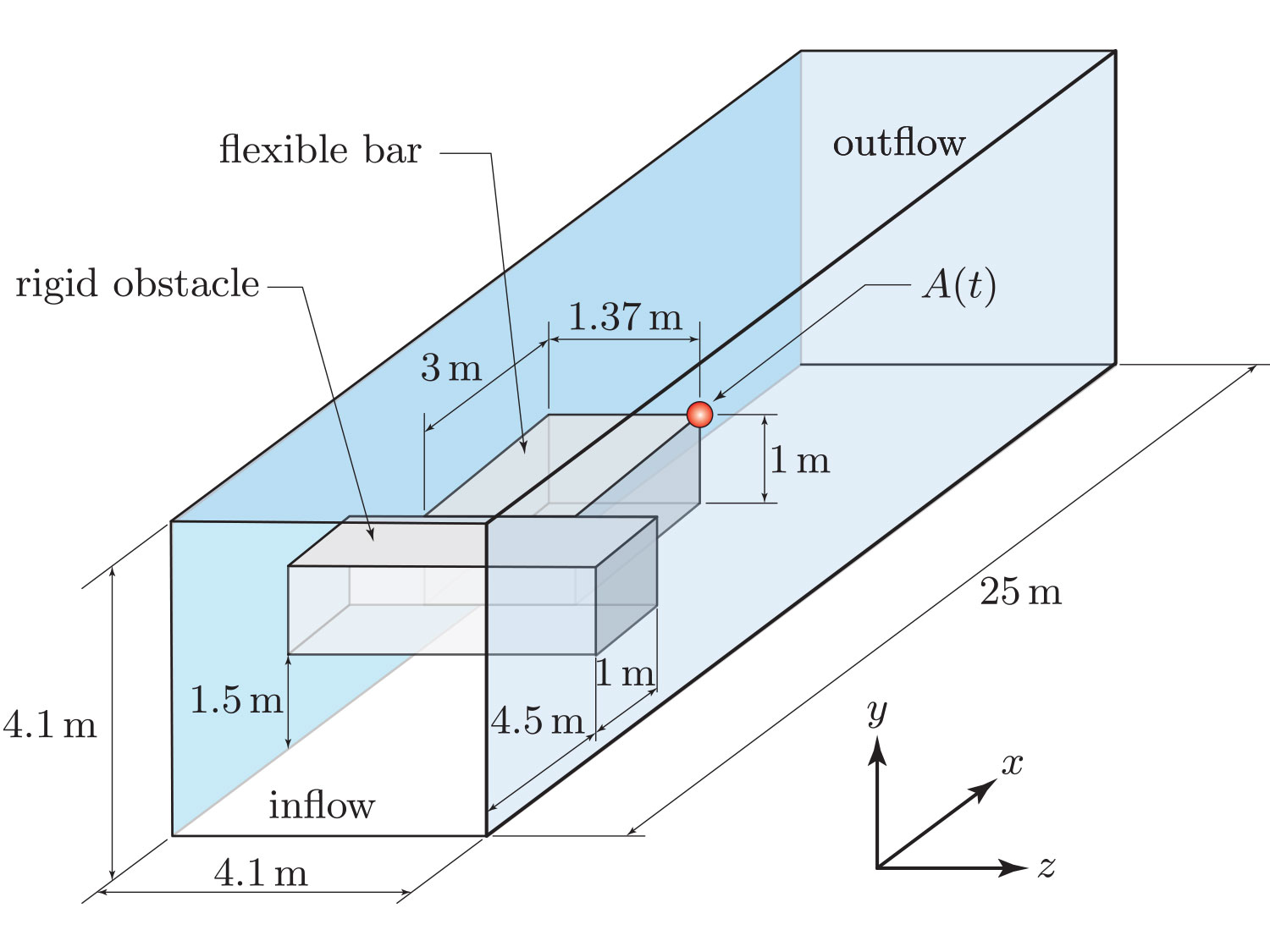
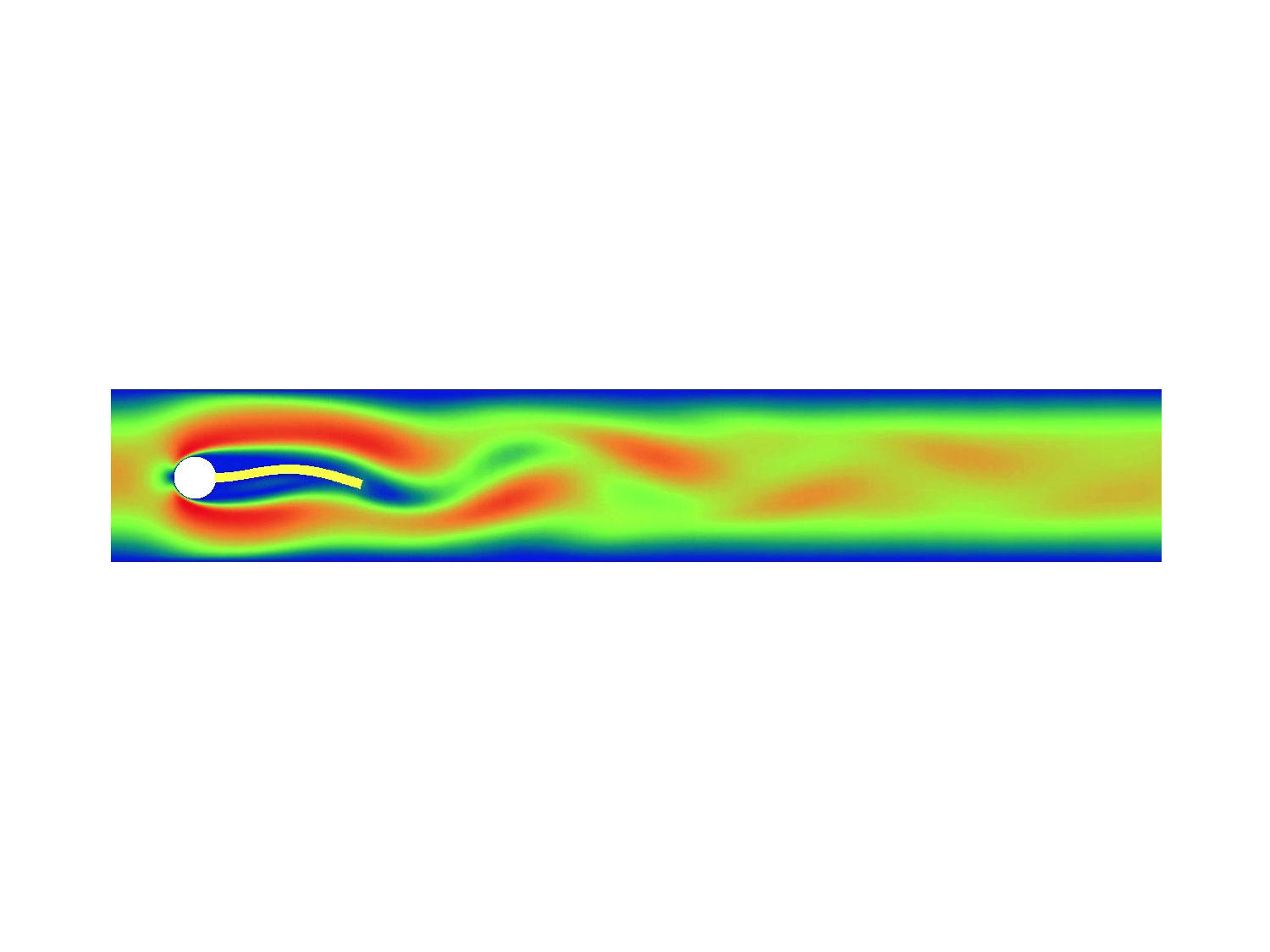
Benchmarking the Immersed Finite Element Method for Fluid-Structure Interaction Problems
FSI problems are very challenging to solve numerically and there are not closed-form solutions that can be generated (say, with the method of manufactured solutions) for the purpose of assessing convergence and computational efficiency. In lieu of closed-formed solutions, the FSI community has de facto agreed to use as benchmarks a collection of numerical tests compiled by Tureck and Hron in 2006. The significance of the above work is that, until now, no immersed method was ever been shown to strictly conform to the Tureck-Hron benchmarks. Costanzo’s group is the first to have produced results conforming to these benchmarks with an immersed method. This accomplishment is extraordinarily important in the FSI community.
Source:
Roy, S., L. Heltai, and F. Costanzo (2015), “Benchmarking the Immersed Finite Element Method for Fluid-Structure Interaction Problems”, Computers and Mathematics with Applications, 69(10), pp. 1167–1188. DOI: 10.1016/j.camwa.2015.03.012.
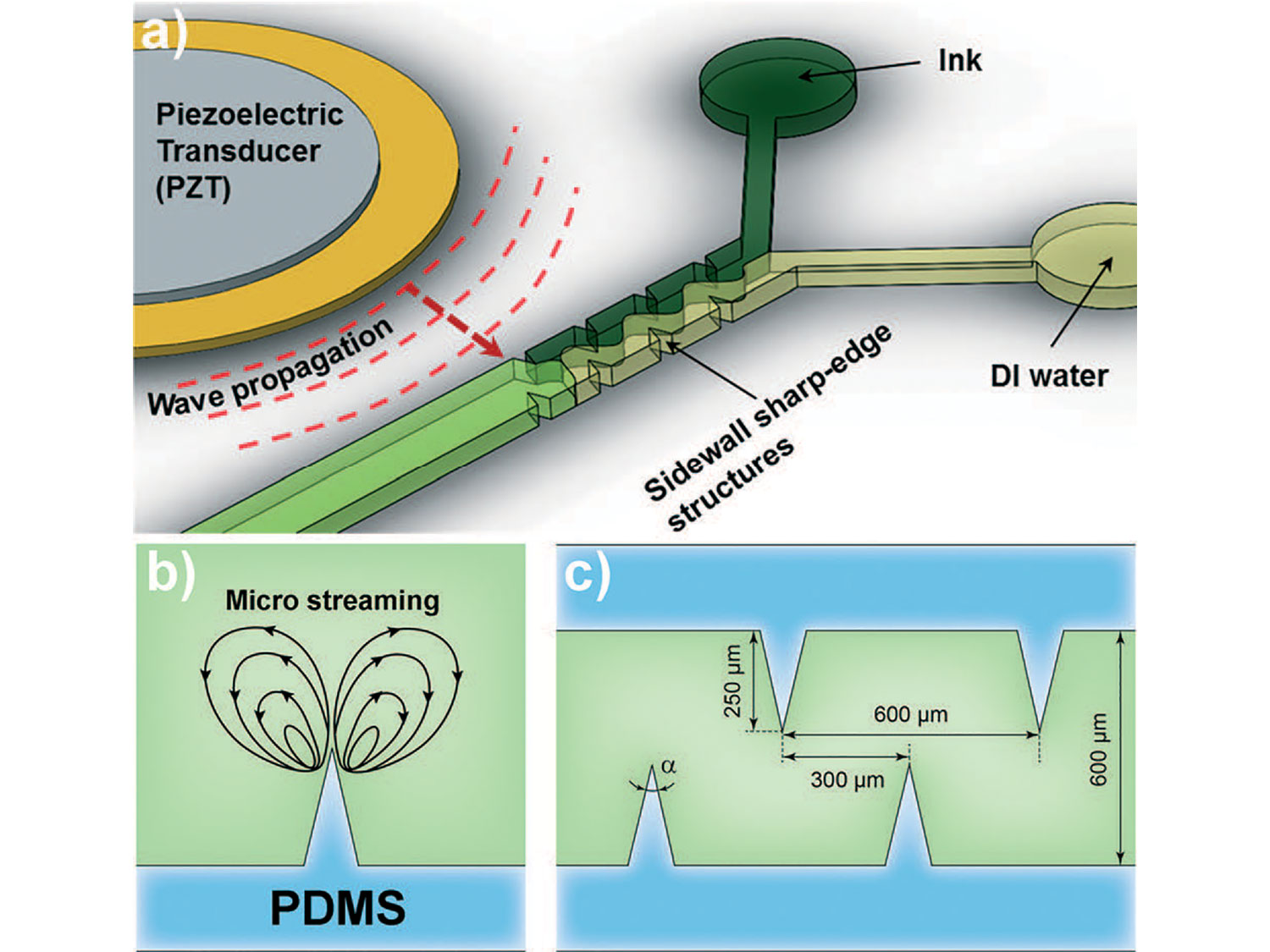
Numerical Study of Acoustophoretic Motion of Particles in a PDMS Microchannel Driven by Surface Acoustic Waves
This paper is focused on the prediction of the forces acting on particles suspended in a streaming flow within a microacoustofluidic device. Studies of the e ects of bulk waves are common. However, the acoustophoretic properties of flows activated by surface acoustic waves are scarce. This paper represents a first rigorous computational study of such motions. This work fits in a general theme of FSI and is currently being generalized to predict the motion of soft inclusions such as cells in microacoustofluidic devices for the purpose of quantifying their mechanical properties.
Source:
Nama, N., R. Barnkob, Z. Mao, C. J. Kähler, F. Costanzo, and T. J. Huang (2015), “Numerical Study of Acoustophoretic Motion of Particles in a PDMS Microchannel Driven by Surface Acoustic Waves”, Lab on a Chip, in press. DOI: 10.1039/C5LC00231A; PMID: 26001199.
(Click images to expand view)
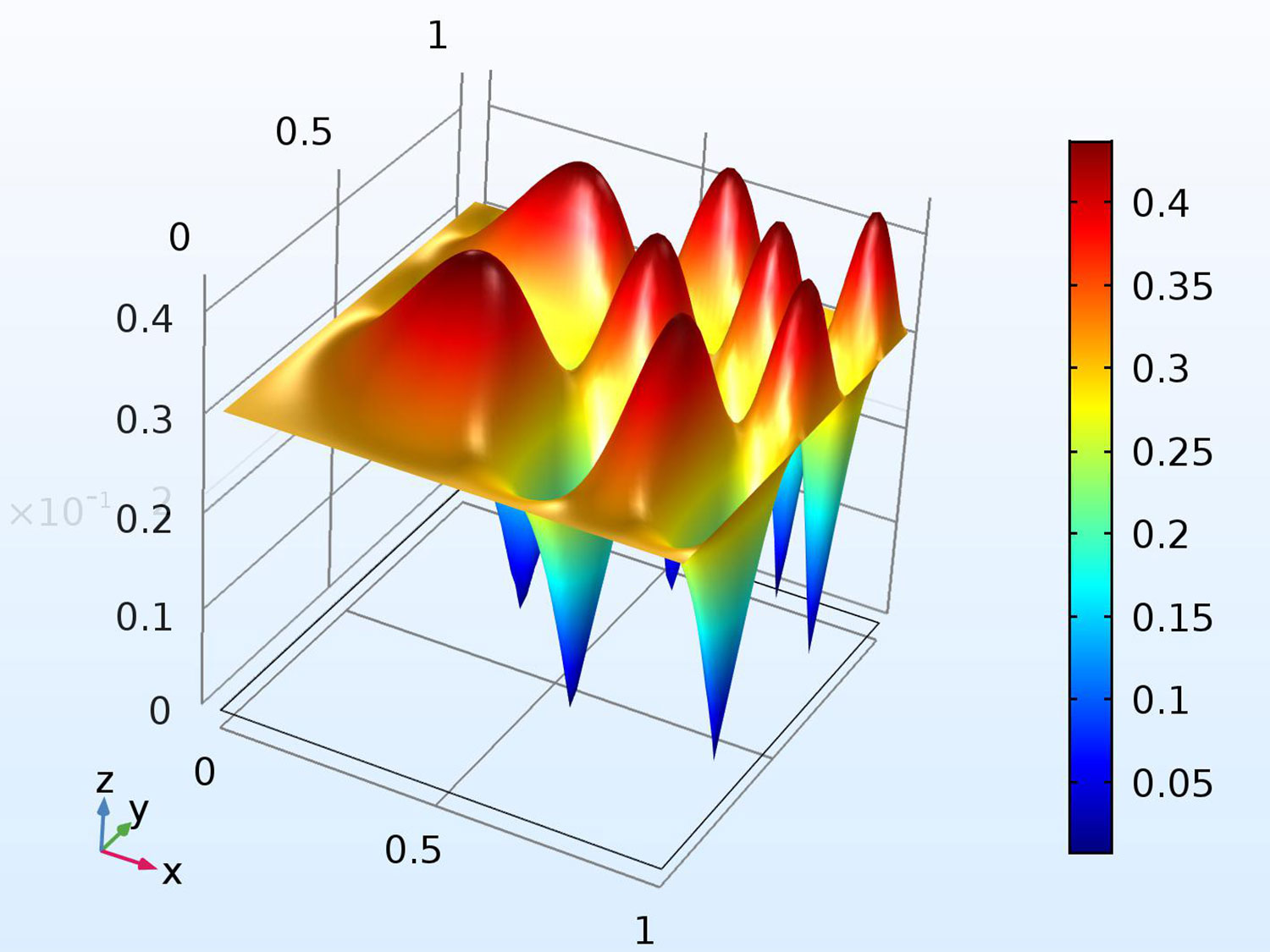
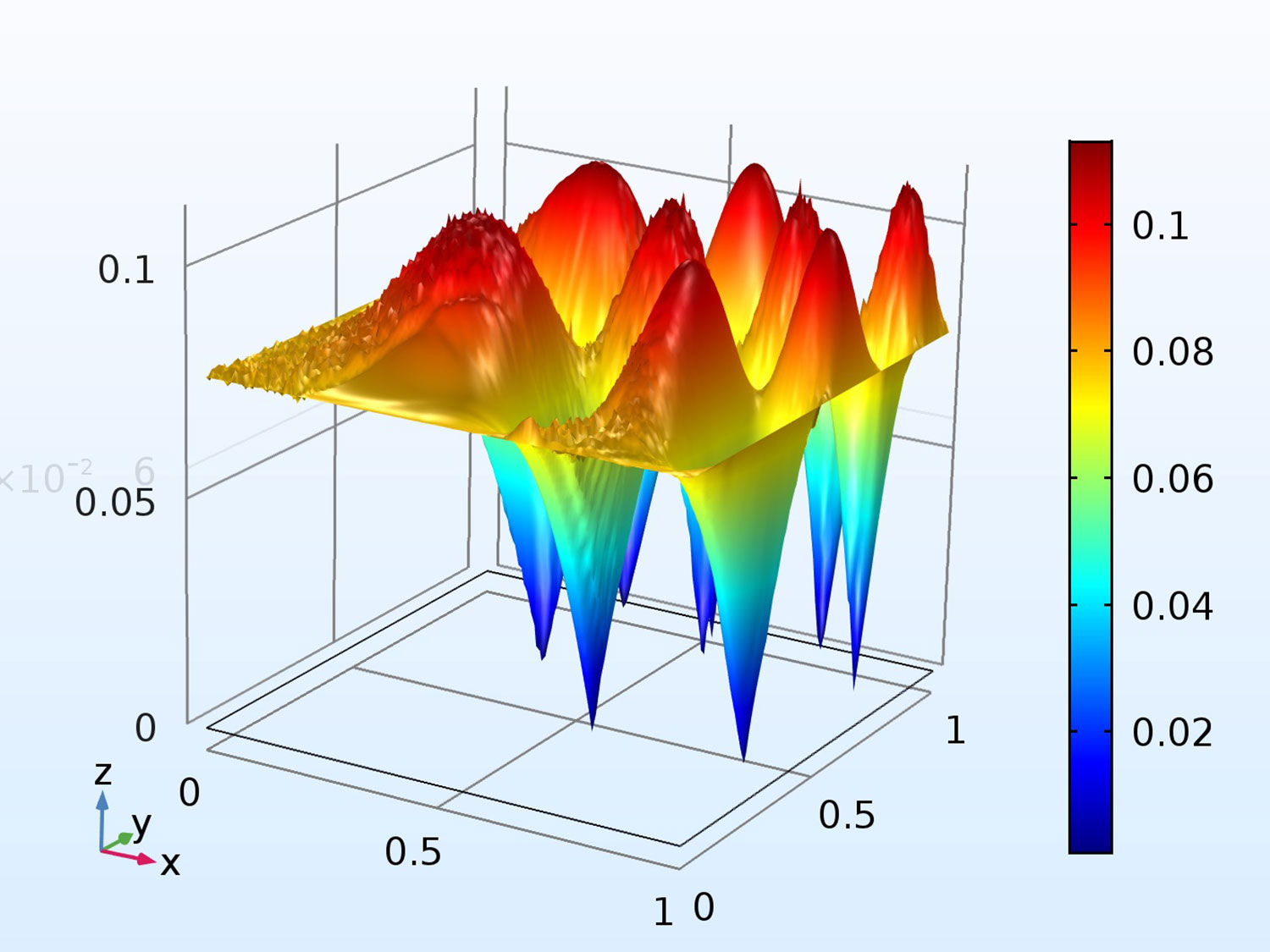
Computational predictions of the trajectories of particles immersed in the fluid filling a micro-fluidic device. The device is excited at MHz frequencies. The trajectories are determined by the excitation conditions (same for all simulations) and the particle size. Acoustophoresis, i.e., the ability to control the motion of particles in a device using sound waves, is at the core of new technologies with strong biomedical applications.
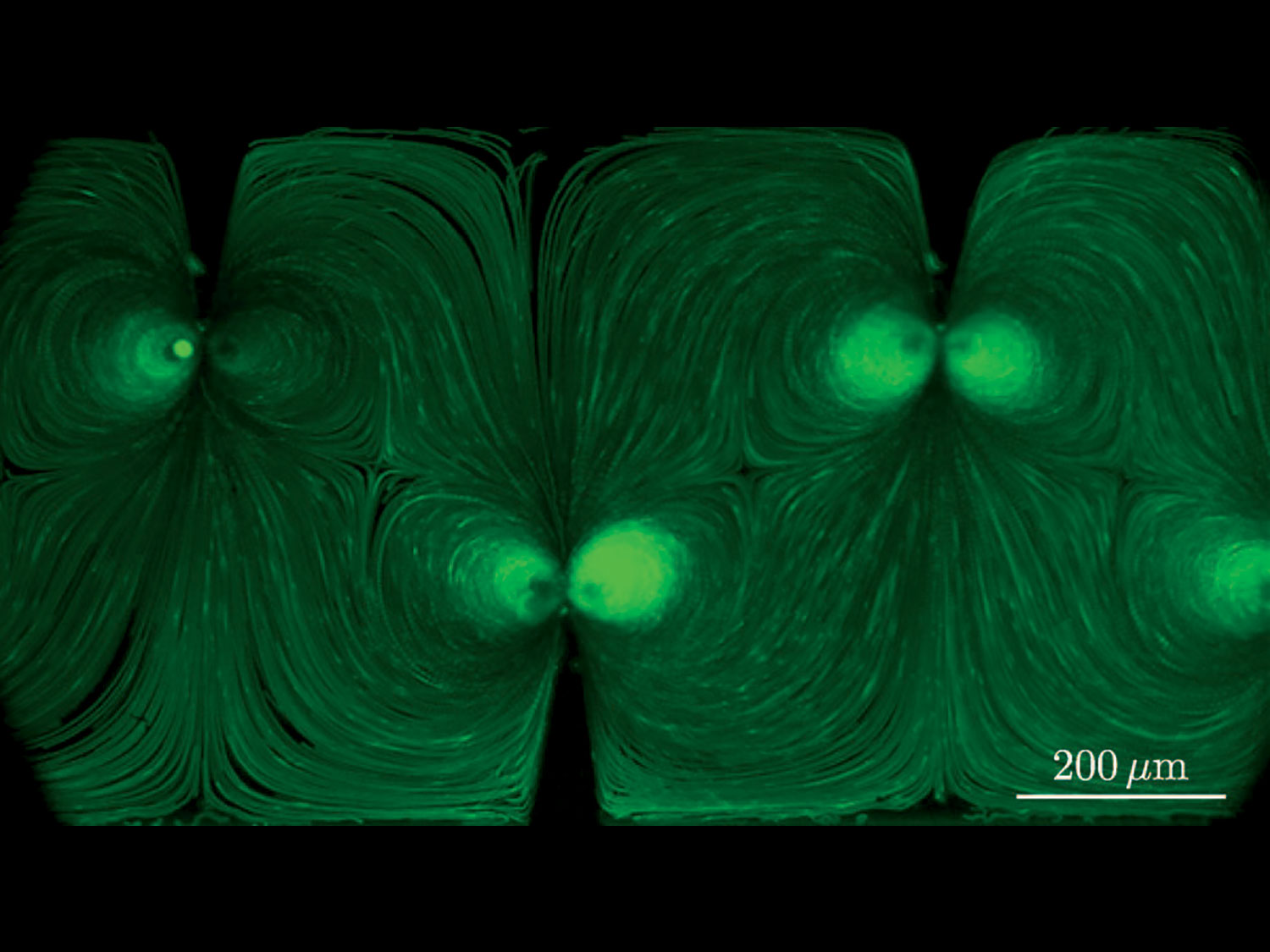
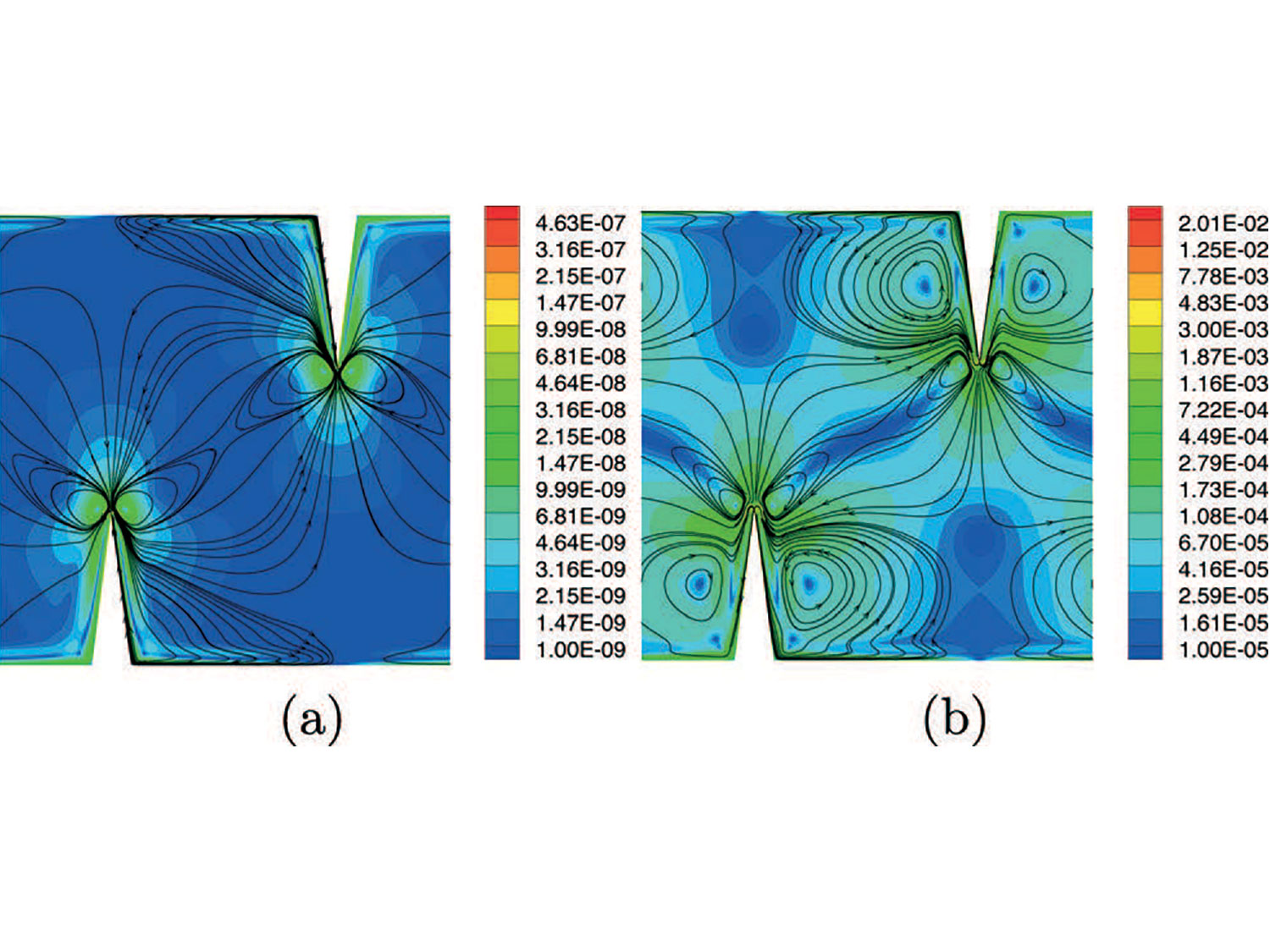
Investigation of Acoustic Streaming Patterns around Oscillating Sharp Edges
Microacoustofluidics deals with the creation of controlled flow patterns for fluids in channels with micron-sized lumen diameter. The flow is activated by high-frequency piezoelectric actu- ators that “shake” the channel and, along with the primary harmonic response, activate fluid flows that are not harmonic and result from the interplay between the dissipative nature of the fluids and the compressible part of their constitutive response. Slow drifts activated by harmonic excitation of fluid have been studied for a long time, but not at the micro-level. More importantly, this field has not received a careful analytical and numerical treatment leaving a large number of technical difficult problems unsolved. This paper predicts streaming flows in a micro-mixer whose channels have walls with has sharp edges. The key innovation here is a singularity analysis for fluid flows analogous to that of stress fields around crack tips in linear elasticity.
Source:
Nama, N., P.-H. Huang, T. J. Huang, and F. Costanzo (2014), “Investigation of Acoustic Streaming Patterns around Oscillating Sharp Edges”, Lab on a Chip, 14(15), pp. 2824– 2836. DOI: 10.1039/c4lc00191e; PMID: 24903475; PMCID: PMC4096312.
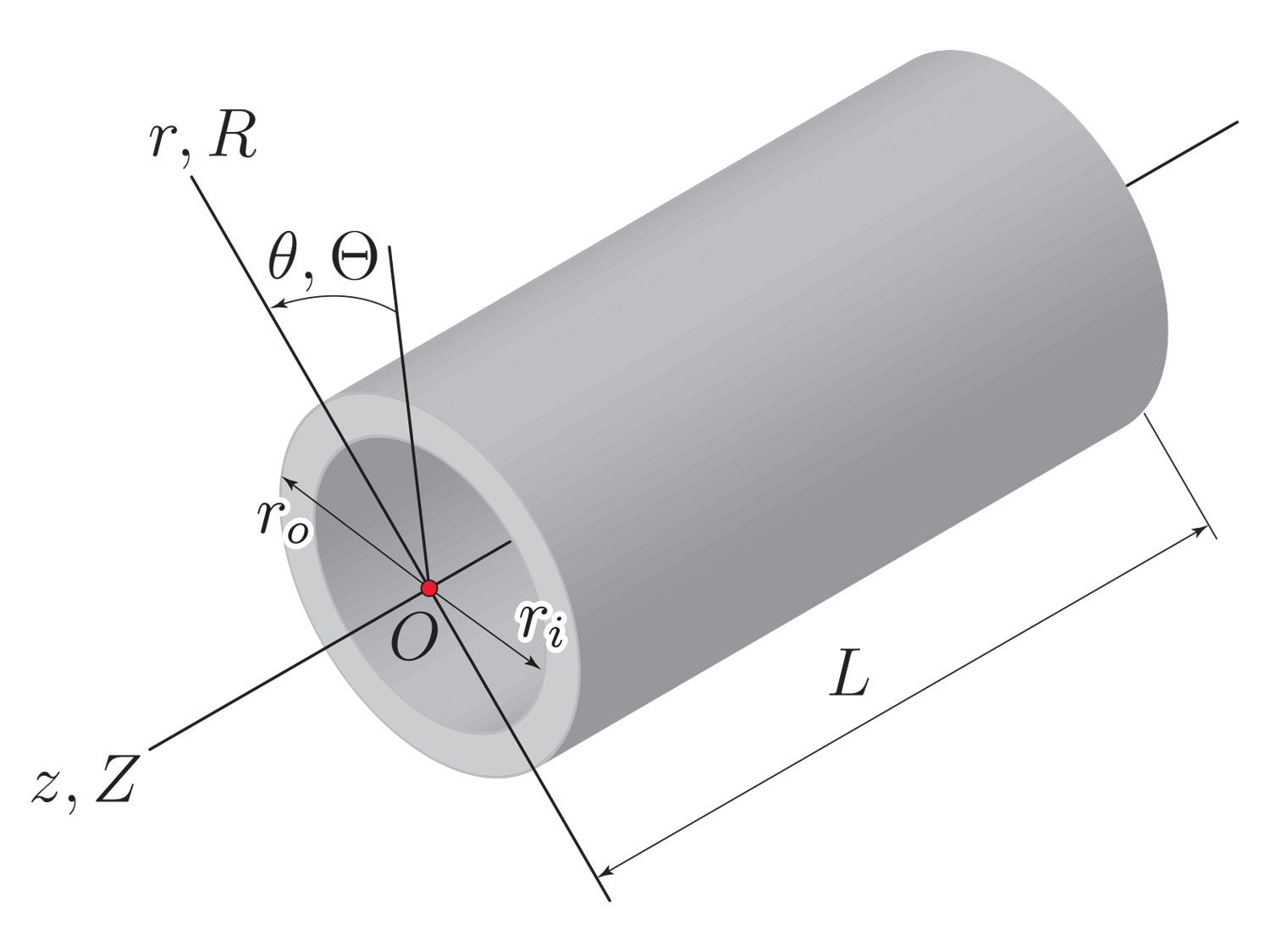
The Invalidity of the Laplace Law for Biological Vessels and of Estimating Elastic Modulus from Total Stress vs. Strain: a New Practical Method
Various mechanical tests are performed in vivo in a clinical setting on tubular organs, like the esophagus. Because of the intrinsic limitations of tests done on live human subjects, these tests provided only limited information. More importantly, for various reasons, the information collected in a clinical setting is routinely interpreted via formulas that are appealing to non- mechanicians, but that are compromised by the quasi-incompressibility of the tissue and the presence of residual stress. In this context, the above paper has provided a re-analysis of the inflation and extension tests of circular cylinders and a re-interpretation of the data collected by common tests so to provide new formulas for the mechanistically correct estimation of the e ective shear modulus of the tissue. The formulas in question require exactly the same input as current clinical practices. However, they present clinicians with a paradigm shift in which the estimate of the tangent moduli (information that is polluted in a quasi-incompressible context) is now replaced by the correct estimation of the tissue’s shear modulus. The work in this paper has the potential to have an strong impact in clinical practice in that it provides clinicians with a methodology to correctly assess the elastic response of tissues of tubular organs in live patients. Drs. Brasseur and Costanzo are now collaborating on an outreach e ort to publicize the new methodology to clinicians.
Source:
Costanzo, F. and J. G. Brasseur (2013), “The Invalidity of the Laplace Law for Biological Vessels and of Estimating Elastic Modulus from Total Stress vs. Strain: a New Practical Method”, Mathematical Medicine & Biology, first published online: September 25, 2013, DOI: 10.1093/imammb/dqt020.
Variational Implementation of Immersed Finite Element Methods
Fluid structure interaction problems in biomedical applications are challenging because one must often model objects that are fully immersed in a fluid and that undergo large displace- ments and rotations in addition to large strains. For example, such is the motion of red blood cells in going from arteries, to arterioles, to capillaries. Immersed methods, originally devel- oped by C. Peskin in the late 1970s for the modeling of blood flow in the hearth, have proven to be far more flexible for biomedical applications than more traditional ALE approaches. Peskin’s approach and later generalizations have su ered from strong limitations, such as the requirement that the immersed body be incompressible with the same density as the surround- ing fluid, the latter also incompressible. The significance of the above paper is the generation of an FEM scheme that is not limited by constitutive assumptions on either the fluid or the solid. Also, it is the first paper that presents a formal proof of the numerical stability of the method. For this reasons the above is a major contribution in the FSI literature.
Source:
Heltai, L. and F. Costanzo (2012), “Variational Implementation of Immersed Finite Element Methods”, Computer Methods in Applied Mechanics and Engineering, 229–232, pp. 110–127.
Office Location
Francesco Costanzo, Ph.D.
Center for Neural Engineering
W-315 Millenium Science Complex
The Pennsylvania State University
University Park, PA 16802
Contact
Phone: 1-814-863-2030
Fax: 1-814-865-9974
Email: fmcostanzo@psu.edu